Диагра́мма рассе́яния (англ. scatter plot), корреляционное поле, форма графического представления данных, использующаяся для выявления возможных, не имеющих строго функционального характера взаимосвязей между количественными переменными.

Первое описание этого графического инструмента М. Френдли и Д. Дэнис (2005) приписывают Дж. Гершелю (John Frederick William Herschel, 1792–1871).

Пусть $X$ и $Y$ – две количественные переменные и наблюдаются $n$ пар значений этих переменных: $(x _{1}, y _{1} ),...,(x _{n}, y _{n} )$. Диаграмма рассеяния – это представление указанных $n$ пар в виде точек на плоскости в прямоугольной системе координат, в которой по оси абсцисс (горизонтальной оси) откладываются значения переменной $Х$, а по оси ординат (вертикальной оси) – значения переменной $Y$, так что на этой диаграмме паре $( x_{i} , y_{i})$ соответствует точка с абсциссой $x_{i}$ и ординатой 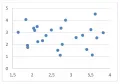$y_{i}$. Рис. 1.Рис. 1.Совокупность точек на диаграмме рассеяния визуально представлена как облако той или иной формы, и по форме этого облака можно делать предварительные выводы о наличии или отсутствии связи между переменными $X$ и $Y$, а также о возможной форме и силе этой связи. Это иллюстрируют приведённые ниже рисунки 1–8.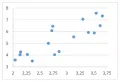Рис. 2.Рис. 2.

Рис. 1 соответствует предположению об отсутствии корреляционной связи между переменными 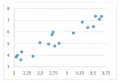$X$ и $Y$. Рис. 3.Рис. 3.На рис. 2 и рис. 3 выявляется тенденция возрастания в среднем значений переменной $Y$ при возрастании значений переменной $X$, что соответствует наличию положительной корреляционной связи между этими переменными; эта связь является более сильной (тесной) на рис. 3.

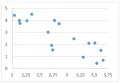Рис. 4. Рис. 4.На рис. 4 и рис. 5 выявляется тенденция убывания в среднем значений переменной $Y$ при возрастании значений переменной $X$, что соответствует наличию отрицательной корреляционной связи между этими переменными; эта связь является более сильной на рис. 5. 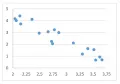Рис. 5. Рис. 5. На рис. 6 проявляется возрастание разброса значений переменной $Y$ с возрастанием значений переменной $X$.

На рисунках 1–6 форма облаков точек на диаграммах указывает на линейный характер связи между переменными $X$ и $Y$, тогда как форма облака на рис. 7 указывает на нелинейный характер связи между переменными. На рис. 8 одна из точек на диаграмме располагается достаточно далеко от облака, образованного остальными точками; наличие на диаграмме подобных точек («выбросов») может указывать на ошибки в представленных данных, так что эти данные следует перепроверить.

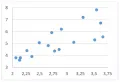Рис. 6.Рис. 6.

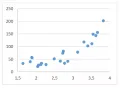Рис. 7.Рис. 7.

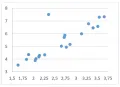Рис. 8.Рис. 8.

Использование диаграммы рассеяния помогает выявлению наличия той или иной формы связи между переменными, однако обнаружение такой зависимости не следует трактовать как обнаружение причинно-следственной связи между рассматриваемыми переменными. Это иллюстрирует следующий пример.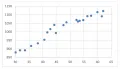Рис. 9.Рис. 9. На рис. 9 показана диаграмма рассеяния, на которой горизонтальная ось соответствует объёму потребительских расходов в Таиланде (млрд долл. США, в постоянных ценах 1970) а вертикальная ось – валовому производству электроэнергии в Российской Федерации (млрд кВт·ч) за период с 2000 по 2020 гг.

На диаграмме выявляется сильная положительная корреляция между рассматриваемыми показателями, которые в действительности не связаны никакими причинно-следственными связями. Рис. 10.Рис. 10.Это типичный пример ложной корреляции, возникающей вследствие того, что динамика каждого из двух показателей имеет выраженный тренд, что можно увидеть на графиках изменения этих показателей (рис. 10 и рис. 11).Рис. 11.Рис. 11.

Обобщением обычной (плоской) диаграммы рассеяния является объёмная диаграмма рассеяния, использующая трёхмерную систему координат, которая позволяет производить визуальный анализ значений трёх переменных. Для анализа большего количества переменных можно использовать перекрывающиеся (составные) диаграммы рассеяния и матрицы диаграмм рассеяния (англ. scatterplot matrix, SPLOM). На перекрывающейся диаграмме рассеяния точки, соответствующие разным парам переменных, отличаются цветом или формой. SPLOM (впервые представил такую визуализацию Дж. Хартиган в 1975) представляет собой матрицу, на диагонали которой находятся гистограммы значений используемых переменных, а внедиагональными элементами являются плоские диаграммы рассеяния, соответствующие разным парам переменных, причём для каждой пары строятся диаграммы рассеяния, отличающиеся выбором переменной, значения которой откладываются на оси абсцисс.