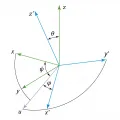
Э́йлеровы углы́ (углы Эйлера), углы $\varphi$, $\psi$, $\theta$, определяющие положение одной декартовой прямоугольной системы координат $Oxyz$ относительно другой декартовой прямоугольной системы координат $Ox'y'z'$ с тем же началом координат и с той же ориентацией. Эйлеровы углы рассматриваются как углы последовательных поворотов одной системы относительно осей другой, после которых обе системы совпадают (см. рисунок). Пусть $u$ – ось, совпадающая с линией пересечения плоскости $Oxy$ с плоскостью $Ox'y'$ и направленная так, что три направления $Oz$, $Oz'$ и $u$ образуют правую тройку. Угол $\psi$ – угол между осями $Ox$ и $u$, отсчитываемый в плоскости $Oxy$ от оси $Ox$ в направлении кратчайшего поворота от $Ox$ к $Oy$; $\theta$ – не превосходящий $\pi$ угол между осями $Oz$ и $Oz'$; $\varphi$ – угол между осями $u$ и $Ox'$, отсчитываемый в плоскости $Ox'y'$ от оси $u$ в направлении кратчайшего поворота $Ox'$ к $Oy'$. Связь между координатами $x,y,z$ и $x',y',z'$:

$$\begin{gathered} x'=(\cos\psi\cos\varphi-\sin\psi\cos\theta\sin\varphi)x'+\\ +(-\cos\psi\sin\varphi-\sin\psi\cos\theta\cos\varphi)y'+(\sin\psi\sin\theta)z',\\ y=(\sin\psi\cos\varphi+\cos\psi\cos\theta\sin\varphi)x'+\\ +(-\sin\psi\sin\varphi+\cos\psi\cos\theta\cos\varphi)y'+(-\cos\psi\sin\theta)z',\\ z=(\sin\theta\sin\varphi)x'+(\sin\theta\cos\varphi)y'+(\cos\theta)z'. \end{gathered}$$Эйлеровы углы введены Л. Эйлером (1748).