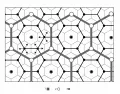
Тео́рия центра́льных мест, совокупность теоретических положений, описывающих пространственную иерархию городского расселения. Создана В. Кристаллером (1932), получила активное развитие в 1960–1970-х гг. Центральные места – поселения, обслуживающие собственное население и население дополнительного района, тем большего, чем выше уровень иерархии. Центральные места образуют в идеальном пространстве многоуровневые правильные гексагональные решётки, тип которых определяется показателем K – числом дополнительных районов следующего, более низкого уровня иерархии, подчинённых одному центральному месту данного уровня (каждое центральное место обладает дополнительными районами всех более низких уровней). Решётка с K=3 (центральные места расположены в узлах решётки) обеспечивает обслуживание территории минимальным числом центральных мест (рис. 1). Число центральных мест на первых пяти уровнях иерархии: 1; 2; 6; 18; 54. Решётка с K=4 (центральные места расположены в серединах рёбер решётки) обеспечивает кратчайшие расстояния в сообщениях между центральными местами (рис. 2). Число центральных мест на первых пяти уровнях иерархии: 1; 3; 12; 48; 192. Построение иерархии с K=7, воплощающей административный принцип (каждое центральное место подчиняется только одному вышестоящему, а не трём или двум) геометрически невозможно (см. рис. 3). Теория не накладывает ограничение на число уровней иерархии, хотя в реальности оно не превышает 7 (исследованная Кристаллером система центральных мест Южной Германии, к которой были условно присоединены сопредельные территории Швейцарии и Австрии). Отмечена тенденция к переходу кристаллеровской иерархии к более высоким значениям K в ходе урбанизации.

Рис. 1. Кристаллеровская решётка с К=3. 1, 2, 3 – центральные места 1, 2 и 3-го уровней иерархии. Иллюстрация: Вячеслав Шупер.Рис. 1. Кристаллеровская решётка с К=3. 1, 2, 3 – центральные места 1, 2 и 3-го уровней иерархии. Иллюстрация: Вячеслав Шупер.

Существуют системы с выпадением отдельных уровней кристаллеровской иерархии, чаще всего 2-го (пример – Венгрия). Постепенно формирующаяся система центральных мест Азиатской России предположительно не будет иметь 1-го уровня, а 2-й будут занимать Большой Новосибирск, включающий Томск, и Большой Владивосток (см. ниже). Эта система будет характеризоваться К=3. Вопрос о перераспределении функций отсутствующих уровней иерархии не имеет единого решения. Теоретически допустимо и формирование рассредоточенных центральных мест, когда два или несколько городов совместно выполняют центральные функции определённого уровня иерархии, имея совокупное население, примерно соответствующее данному уровню. В перспективе 15-20 лет возможно формирование в системе центральных мест Центрального федерального округа 2-го уровня, ныне отсутствующего, в составе четырёх рассредоточенных центральных мест (при К=5, см. ниже): Ярославль – Кострома – Рыбинск; Владимир – Ковров – Иваново; Тула – Новомосковск – Калуга – Обнинск и Воронеж – Липецк – Елец. Однако это потребует значительно более высокого уровня развития транспортной инфраструктуры. Например, экспрессное сообщение должно сделать возможными поездки из Ярославля в Москву примерно за час и поездки из Костромы и Рыбинска в Ярославль также в пределах часа. В таком случае жители Ярославля смогут ездить на работу в Москву, а жители Костромы и Рыбинска – в Ярославль. Распространение удалённой занятости облегчит формирование рассредоточенных центральных мест. 

Другая важнейшая характеристика систем центральных мест – k, доля центральных мест в населении дополнительного района. Она одинакова для всех уровней иерархии, поскольку отсутствие этой аксиомы и аксиомы о постоянном K приводит к парадоксу: население центральных мест более низких уровней иерархии может превышать этот показатель для более высоких уровней. Соотношение людностей центральных мест смежных уровней описывается уравнением Беккманна – Парра: p_m/p_m+1=(K-k)/(1-k), где p_m – людность центрального места уровня иерархии m; p_m+1 – то же для следующего нижележащего уровня m+1. Расстояния между центральными местами уменьшаются при переходе на один уровень вниз в √K раз. Характерное пространство систем центральных мест 10⁴–10⁵ км² подвержено историческим изменениям: с прогрессом транспортного сообщения оно увеличивается, а число уровней иерархии сокращается. Формирование систем центральных мест занимает многие десятилетия и даже столетия: сначала система городского расселения складывается как целостность, при этом она начинает всё более соответствовать правилу «ранг – размер», затем формируется иерархическая структура, что приводит к отклонению от этого правила и установлению большего соответствия теории центральных мест. Бурное развитие субурбанизации и рурбанизации приводит к размыванию центральных мест, которые уже не допускают точечного представления в масштабе характерного пространства их систем, что потребовало разработки варианта теории центральных мест, в котором учитывается их площадь, – центральные места и их дополнительные районы образуют континуум, а вся система центральных мест страны или региона представляет квазирельеф с поднятиями, в том числе очень резкими, и понижениями.

Теорию центральных мест часто отождествляют с теорией экономического ландшафта А. Лёша, однако объединение этих теорий некорректно, поскольку они имеют разную аксиоматику. В теории центральных мест пространство изотропно, экономическому ландшафту анизотропность присуща имманентно. Системы центральных мест формируются затратами времени на передвижение, особенно значим суточный цикл, экономические ландшафты состоят из рыночных зон, их определяют транспортные издержки. Лёш был хорошо знаком с теорией центральных мест и подробно излагал её в своей книге как близкую, но другую теорию. Сведений о знакомстве В. Кристаллера с книгой Лёша нет.

Развитие теории центральных мест, как и любой формализованной теории, предполагает отход от наглядных представлений на определённом уровне сложности. Последнее позволяет рассматривать и другие варианты кристаллеровской иерархии, кроме как с К=3 и К=4. Так, в Тихоокеанской России (в границах Дальневосточного федерального округа, 2017) в перспективе может сформироваться система центральных мест с К=2. Это вырожденный случай кристаллеровской иерархии, где на 1-м уровне будет Большой Владивосток с населением, включая агломерацию, 1,3 – 1,5 млн жителей, на 2-м – Хабаровск, на 3-м – Якутск и Благовещенск, на 4-м – Комсомольск-на-Амуре, Южно-Сахалинск, Петропавловск-Камчатский и Магадан. Такая вырожденная система центральных мест будет охватывать территорию в 10⁶ км². В настоящее время система центральных мест Тихоокеанской России ещё не сложилась – все центры субъектов федерации, кроме Биробиджана, тяготеют к Москве сильнее, чем к Владивостоку или Хабаровску.

Для описания неравномерного городского расселения разработан релятивистский вариант теории центральных мест. Он предполагает взаимозависимость между людностью центральных мест и их положением в пространстве, т. е. релятивизирует эти показатели. Уровни иерархии подразделяются на тяжёлые и лёгкие, имеющие людность выше или ниже теоретически предсказанной. Они чередуются. Как правило, нечётные уровни, начиная с 1-го, тяжёлые, а чётные – лёгкие. Тяжёлые уровни, сдвигаясь к границам региона, охватываемого системой центральных мест, а лёгкие, напротив, сгущаясь вокруг главного центра, взаимно уравновешивают друг друга, вследствие чего система находится в состоянии изостатического равновесия. Соответственно, образование крупных городских агломераций – результат не притяжения города-гиганта, а неравномерности сети городского расселения в регионе площадью 10⁴–10⁵ км². Именно поэтому не сформировались крупные городские агломерации вокруг Минска или Будапешта, сосредоточивающих примерно пятую часть населения своих стран, – разница в людности тяжёлых и лёгких уровней в Белоруссии и Венгрии невелика, а сети городского расселения этих стран относительно равномерны. Наоборот, практически все города, образовавшие огромную Московскую агломерацию, – Подольск, Мытищи, Балашиха, Люберцы, Химки и др. – относятся к очень лёгкому 4-му уровню иерархии Московского столичного региона, по территории близкого к Центральному экономическому району. Релятивистский вариант теории применим также к системам размытых и рассредоточенных центральных мест.

В случае максимального проявления агломерационных эффектов центральные места полностью утрачивают дополнительные районы, вследствие чего уравнение Беккманна – Парра теряет смысл: k = 1, а деление на 0 невозможно. В этом случае людности центральных мест смежных уровней иерархии находятся в соотношении, равном К. Тогда суммарная людность центральных мест для всех иерархических уровней, кроме 1-го, становится одинаковой. Теоретически возможны иерархии с дробным значением К, однако этот вопрос ещё не изучен. См. также статью Теоретическая география.