Преде́л О́ппенге́ймера – Во́лкова, верхний предел массы нейтронной звезды, при которой она может существовать как холодный невращающийся объект. Предел Оппенгеймера – Волкова определяется условием равенства сил гравитации, сжимающих нейтронную звезду, и сил давления вырожденного газа нейтронов внутри неё, противодействующих гравитационному сжатию. Нейтронные звёзды, массы которых превышают этот предел, претерпевают гравитационный коллапс с образованием чёрных дыр.

Нейтронные звёзды являются конечным продуктом эволюции звёзд с начальной массой, лежащей в интервале примерно от 12 до 30 $M_\odot$ (где $M_\odot$ – масса Солнца). После выгорания водорода и гелия в ходе термоядерных реакций в недрах таких звёзд образуется невырожденное углеродно-кислородное ядро, в котором стационарное термоядерное горение продолжается вплоть до образования химических элементов «железного пика», имеющих максимальную энергию связи. После этого выделение тепла при ядерных реакциях прекращается, ядро сжимается и теряет динамическую устойчивость, коллапсируя вплоть до образования устойчивой нейтронной звезды, состоящей из вырожденного газа нейтронов и гиперонов.

Когда плотность $\rho$ нейтронного газа начинает превышать граничное значение $\rho_b^n\approx6,\!2\cdot10^{15}\ г/см^3,$ он становится релятивистским. При этом граничная энергия нейтронов (энергия Ферми)  становится равной энергии покоя нейтрона $m_nc^2$ (где $m_n$ – масса нейтрона, $c$ – скорость света в вакууме), а граничный Ферми-импульс, определяемый соотношением

$$p_{fe}^n=\left(\frac{3\rho}{8\pi m_n}\right)^{1/3}2\pi\hbar\approx\left(\frac{\rho}{\rho_b^n}\right)^{1/3}m_nc,$$становится равным $p_{fe}^n=m_nc.$ Когда плотность вырожденного вещества значительно превышает $\rho_b^n,$ нейтроны становятся ультрарелятивистскими, $p_{fe}^n\!\gg\!m_nc.$ Уравнение состояния, связывающее давление $P$ и плотность $\rho$ вырожденного газа нейтронов, в предельных случаях нерелятивистских и ультрарелятивистских нейтронов является степенным (политропным) и имеет, соответственно, вид $P\!=\!K_1\rho^{5/3}$ и $P\!=\!K_2\rho^{4/3}$ (где $K_1$ и $K_2$ – коэффициенты, зависящие от фундаментальных физических констант и химического состава вещества).

В рамках нерелятивистской теории гравитации (закона всемирного тяготения И. Ньютона), когда гравитационные силы определяются только массой покоя частиц, плотность вещества не ограничена. В предельном случае ультрарелятивистских нейтронов максимальная масса нейтронной звезды составляла бы

$$M=25,\!36\left(\frac{K_2}{\pi G}\right)^{3/2},$$где G – гравитационная постоянная. Для ультрарелятивистских нейтронов коэффициент $K_2$ равен

$$K_2=\frac{\left(3\pi^2\right)^{1/3}}{4}\frac{c\hbar}{{m_n}^{4/3}},$$где $\hbar$ – постоянная Планка. Таким образом, предельная масса оказывается равной предельной массе водородного белого карлика

$$M_{пред}\approx5,\!83\,M_\odot.$$Однако значение гравитационного потенциала внутри и на поверхности нейтронной звезды сравнимо с квадратом скорости света, вследствие чего для описания создаваемых ею гравитационных сил необходимо использовать общую теорию относительности (ОТО) А. Эйнштейна вместо нерелятивистского закона всемирного тяготения. В рамках ОТО при уменьшении размера звезды создаваемые ею гравитационные силы растут быстрее, чем в нерелятивистской теории гравитации. Вследствие этого, а также из-за участия в гравитационном взаимодействии полной энергии элементарных частиц (а не только их энергии покоя) нейтронная звезда теряет устойчивость значительно раньше, чем нейтроны станут ультрарелятивистскими, при плотности около 10¹⁵ г/см³. Вследствие этого значение предельной массы нейтронной звезды в релятивистской теории гравитации существенно меньше, чем в нерелятивистской.

Зависимость массы нейтронной звезды от её центральной плотности согласно расчётам Р. Оппенгеймера и Дж. Волкова 1939 г. в рамках общей теории относительности для идеального газа нейтронов. Максимальная масса (предел Оппенгеймера – Волкова) в этой модели составляет 0,7 массы Солнца. По вертикальной оси отложена масса нейтронной звезды в массах Солнца. По горизонтальной оси отложена безразмерная функция энергии Ферми-нейтронов, связанная с их концентрацией (верхняя шкала), и её арктангенс (нижняя шкала). График из статьи: J. R. Oppenheimer and G. M. Volkoff, On Massive Neutron Cores, 1939, Phys. Rev., V. 55, P. 374–381. Адаптация: БРЭ. 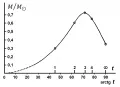© 1939 American Physical SocietyЗависимость массы нейтронной звезды от её центральной плотности согласно расчётам Р. Оппенгеймера и Дж. Волкова 1939 г. в рамках общей теории относительности для идеального газа нейтронов. Максимальная масса (предел Оппенгеймера – Волкова) в этой модели составляет 0,7 массы Солнца. По вертикальной оси отложена масса нейтронной звезды в массах Солнца. По горизонтальной оси отложена безразмерная функция энергии Ферми-нейтронов, связанная с их концентрацией (верхняя шкала), и её арктангенс (нижняя шкала). График из статьи: J. R. Oppenheimer and G. M. Volkoff, On Massive Neutron Cores, 1939, Phys. Rev., V. 55, P. 374–381. Адаптация: БРЭ. © 1939 American Physical SocietyВ 1939 г. Р. Оппенгеймер и Дж. Волков рассмотрели звезду, состоящую из холодного вырожденного идеального газа нейтронов (т. е. без учёта сил отталкивания между нейтронами), и в рамках ОТО вывели уравнение равновесия такой звезды. В результате его решения они получили для предельной массы нейтронной звезды значение около $0,\!7\,M_\odot,$ соответствующее центральной плотности вещества примерно 10¹⁵ г/см³ (рисунок). Эта оценка предельной массы более чем в 2 раза меньше предельной массы углеродно-кислородного белого карлика (предела Чандрасекара). В этих условиях гравитационный коллапс любых звёзд массой более $0,\!7\,M_\odot$ не остановился бы на стадии нейтронной звезды, а продолжился бы дальше с образованием чёрной дыры. Образование нейтронных звезд на последних стадиях звёздной эволюции было бы невозможным, как и вообще их существование во Вселенной.

Однако к концу 1950-х гг. стало известно, что при сверхъядерных плотностях, $\rho>3\cdot10^{14}\ г/см^3,$ вещество становится сильно неидеальным, между нуклонами начинают действовать силы отталкивания, которые уменьшают сжимаемость вещества и увеличивают его давление по сравнению с тем, что имеет место в идеальном вырожденном нейтронном газе. Это может существенно увеличить предел массы нейтронной звезды и сделать её существование возможным. Используя накопившиеся к тому времени знания из области ядерной физики, А. Камерон в 1959 г. вычислил предельную массу нейтронной звезды, получив значение около $2\,M_\odot$ (Cameron, 1959).

Тем не менее по состоянию на 2022 г. точный расчёт уравнения состояния нейтронной звезды при столь высоких плотностях, учитывающий как релятивистские эффекты гравитации, так и силы отталкивания между нуклонами, ещё не удалось провести. Предложено порядка 10 различных вариантов уравнения состояния, которые, согласно работам В. А. Амбарцумяна и Г. С. Саакяна (Амбарцумян, 1961), а также Р. Мэлоуна, М. Джонсона (США) и Х. Бете (Malone, 1975) приводят к максимальной массе нейтронной звезды в интервале от 1,1 до 1,9 $M_\odot.$ Теоретический предел массы нейтронной звезды, вычисленный в 1974 г. в рамках ОТО без уточнения уравнения состояния вещества и при условии выполнения принципа причинности (скорость звука меньше скорости света), оказался равен $3,\!2\,M_\odot$ (Rhoades, 1974).

На основе наблюдений всплеска гравитационных волн GW170817, произошедшего в результате слияния двух нейтронных звёзд и наблюдавшегося в 2017 г., был сделан вывод, что предельная масса холодной нейтронной звезды составляет около $2,\!16\,M_\odot$ (Most, 2018). Более надёжная наблюдательная оценка возможной предельной массы нейтронной звезды была получена по результатам наблюдений двойного пульсара PSR J038+0432. Измеренная масса входящей в его состав нейтронной звезды составляет примерно $2,\!01\,M_\odot$ (Demorest, 2010). По состоянию на 2022 г. эта величина является максимальной измеренной массой нейтронной звезды.