Предел Чандрасекара
Преде́л Чандрасека́ра, верхний предел массы, при которой звезда может существовать как холодный невращающийся белый карлик. Предел Чандрасекара определяется условием равенства сил гравитации, сжимающих белый карлик, и сил давления вырожденного газа электронов внутри него, противодействующих гравитационному сжатию. Если масса звезды превышает предел Чандрасекара, то давление вырожденного электронного газа не может сдерживать гравитационное тяготение и звезда в процессе своей эволюции претерпевает гравитационный коллапс и становится нейтронной звездой или чёрной дырой.
Белые карлики являются конечным продуктом эволюции звёзд с начальной массой не превышающей примерно (где – масса Солнца). Если масса звезды лежит в интервале то после выгорания водорода и гелия в ходе термоядерных реакций в недрах таких звёзд у них образуется углеродно-кислородное ядро с массой порядка Затем внешние слои звезды сбрасываются в окружающее пространство, становясь планетарной туманностью, а обнажившееся ядро превращается в белый карлик. Если начальная масса звезды не превышает то в её ядре не достигается температура термоядерного горения гелия, и в результате возможно образование маломассивного гелиевого белого карлика. Однако время эволюции звезды вплоть до его образования может превышать возраст Вселенной. Таким образом, наблюдаемые белые карлики, которые, возможно, состоят из гелия, являются, по всей вероятности, продуктом эволюции тесной двойной звезды, в которой происходило интенсивное перетекание вещества с одного из компонентов, обнажившее его маломассивное гелиевое ядро.
Вследствие большой плотности вещество белого карлика оказывается вырожденным настолько сильно, что влияние температуры на давление вещества, противодействующее гравитации, оказывается пренебрежимо малым. Поэтому давление вырожденного газа электронов в белом карлике зависит только от его плотности которая тем выше, чем больше масса белого карлика. Ввиду принципа Паули в вырожденном веществе с ростом плотности электроны занимают всё более высокие энергетические состояния, вследствие чего растёт кинетическая энергия электронов, определяющая давление. Когда плотность начинает превышать граничное значение (где – число барионов, приходящееся на один электрон), электронный газ становится релятивистским. При этом граничная энергия электронов (энергия Ферми) становится равной энергии покоя электрона (где – масса электрона, – скорость света в вакууме), а граничный Ферми-импульс, определяемый соотношением
становится равным (здесь – масса протона, – постоянная Планка). Для водорода для гелия и всех химических элементов, у которых атомные ядра состоят из альфа-частиц (например, ядро углерода состоит из трёх альфа-частиц, кислорода – из четырёх и т. д.), Таким образом, веществу белого карлика соответствует Когда плотность вырожденного вещества значительно превышает граничное значение электроны становятся ультрарелятивистскими:
Уравнение состояния связывающее давление и плотность газа вырожденных электронов и ядер, в котором давление ядер много меньше электронного, впервые получено в работах Р. Фаулера (Fowler, 1926) и Я. И. Френкеля (Frenkel, 1928) для случая нерелятивистских электронов и обобщено в работе Э. Стонера (Stoner, 1930) для больших плотностей, при которых важны релятивистские эффекты специальной теории относительности. В предельных случаях нерелятивистских и ультрарелятивистских электронов уравнение состояния получается степенным (политропным) и имеет, соответственно, вид и (где и – коэффициенты, зависящие от фундаментальных физических констант и химического состава вещества).
В звезде, находящейся в состоянии равновесия, при заданном уравнении состояния её вещества можно легко найти зависимость массы звезды от плотности вещества (средней или центральной). Из уравнения гидростатического равновесия и уравнения неразрывности получаются следующие соотношения (все физические константы приняты равными единице):
где и – масса и радиус звезды, – показатель политропы в уравнении состояния вещества белого карлика (равный 5/3 для нерелятивистских и 4/3 для ультрарелятивистских электронов). Таким образом, чем больше масса белого карлика, тем сильнее он сжимается под действием собственной гравитации и, соответственно, тем выше его плотность. При не слишком больших массах и плотностях электроны в белом карлике являются нерелятивистскими и в этом случае связь между массой и плотностью имеет следующий вид: С увеличением плотности до очень больших значений электроны становятся ультрарелятивистскими, показатель политропы в уравнении состояния стремится к значению 4/3 а масса белого карлика при этом стремится к постоянному пределу, который принято называть чандрасекаровским (см. рисунок).
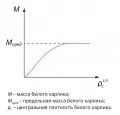 Зависимость массы белого карлика от его центральной плотности. С ростом плотности масса стремится к предельной массе (пределу Чандрасекара), равной 1,46 массы Солнца.Первая оценка предельной массы белого карлика была сделана Э. Стонером в той же работе 1930 г., где он использовал модель с постоянной плотностью и получил значение для В 1931 г. С. Чандрасекар существенно уточнил предельное значение массы, используя равновесную модель политропного газа с применимую к ультрарелятивистскому электронному газу, получив для того же значения (Chandrasekhar, 1931). Результаты численных расчётов этой модели для различных значений были опубликованы Р. Эмденом в 1907 г. Ввиду углеродно-кислородного состава вещества белых карликов ему соответствует и, следовательно, Это значение было впервые получено в работе Л. Д. Ландау (Landau, 1932; русский перевод: Ландау, 2008), который использовал ту же политропную модель с и Полученная Эмденом связь массы белого карлика с коэффициентом , в рамках единственной равновесной политропной модели для имеет следующий вид:
Зависимость массы белого карлика от его центральной плотности. С ростом плотности масса стремится к предельной массе (пределу Чандрасекара), равной 1,46 массы Солнца.Первая оценка предельной массы белого карлика была сделана Э. Стонером в той же работе 1930 г., где он использовал модель с постоянной плотностью и получил значение для В 1931 г. С. Чандрасекар существенно уточнил предельное значение массы, используя равновесную модель политропного газа с применимую к ультрарелятивистскому электронному газу, получив для того же значения (Chandrasekhar, 1931). Результаты численных расчётов этой модели для различных значений были опубликованы Р. Эмденом в 1907 г. Ввиду углеродно-кислородного состава вещества белых карликов ему соответствует и, следовательно, Это значение было впервые получено в работе Л. Д. Ландау (Landau, 1932; русский перевод: Ландау, 2008), который использовал ту же политропную модель с и Полученная Эмденом связь массы белого карлика с коэффициентом , в рамках единственной равновесной политропной модели для имеет следующий вид:
где – гравитационная постоянная. Для ультрарелятивистских электронов коэффициент равен
где – атомная единица массы. Таким образом, предельная масса оказывается равной
что для даёт значение
В природе предельная масса белого карлика, полученная выше, не достигается, т. к. уже при большой, но конечной плотности появляются факторы, приводящие к отклонениям от политропного уравнения состояния и к изменению гравитационной силы. При большой плотности атомные ядра начинают захватывать электроны (нейтронизация), что замедляет рост давления при росте плотности, а при больших значениях гравитационного потенциала к ньютоновской гравитации добавляются эффекты общей теории относительности, увеличивающие рост гравитационной силы с уменьшением радиуса. Оба эти эффекта приводят к тому, что предельная масса белого карлика уменьшается на несколько процентов. Точное значение этого уменьшения зависит от химического состава, определяющего плотность начала нейтронизации.
Название «предел Чандрасекара» в значительной степени условно, т. к. в его установление сравнимый вклад внесли Э. Стонер и Л. Д. Ландау. Однако в последующие годы, работая в Англии и США, С. Чандрасекар получил важные результаты в теории белых карликов, включая их связи с астрономическими наблюдениями, тогда как Стонер и Ландау больше не работали в этой области. Свою роль сыграл также спор Чандрасекара с А. Эддингтоном, который утверждал, что в процессе эволюции звезда потеряет много массы и превратится в белый карлик докритической массы. Чандрасекар же отстаивал реальность и достижимость этого предела, а также наступление гравитационного коллапса более массивной звезды. В итоге он оказался прав. Этот спор способствовал переезду Чандрасекара в 1937 г. на работу из Англии в США, где он чрезвычайно плодотворно работал в разных областях физики и астрофизики около 40 лет, став в 1983 г. лауреатом Нобелевской премии по физике за «теоретические работы по изучению физических процессов, которые играют важную роль для строения и эволюции звёзд» (The Nobel Prize in Physics 1983).
