Подъёмная си́ла, одна из составляющих полной аэродинамической силы, действующей на тело, движущееся в газе или жидкости; направлена перпендикулярно вектору скорости тела (рис. 1).

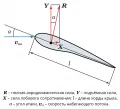Рис. 1. Силы, действующие на крыло.Рис. 1. Силы, действующие на крыло.Действует на крыло и фюзеляж летящего самолёта, глиссирующего по воде судна и др. Вызвана наложением на набегающий потенциальный (безвихревой) поток (рис. 2, а) циркуляционного потока (рис. 2, б), возникающего вокруг обтекаемого профиля (например, крыла). 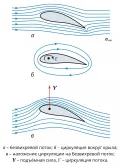Рис. 2. Образование подъёмной силы.Рис. 2. Образование подъёмной силы.Вследствие такого наложения (рис. 2, в) на верхней стороне крыла скорость потока увеличивается, а на нижней – уменьшается. Из уравнения Бернулли следует, что давление над крылом уменьшается, а под крылом – увеличивается, т. е. возникает сила, действующая на крыло снизу вверх, – подъёмная сила.

В 1904 г. Н. Е. Жуковский и позднее немецкий математик В. Кутта теоретически получили выражение для подъёмной силы $Y$ крыла, обтекаемого потенциальным потоком идеальной несжимаемой жидкости: $Y=ρv_∞Γ$, где $ρ$ – плотность жидкости, $v_∞$ – скорость набегающего потока, $Γ$ – скалярная величина, описывающая циркуляцию потока вокруг крыла. Эта формула называется формулой Жуковского или Жуковского – Кутты. Причиной возникновения циркуляции является образование поверхности раздела между потоками, стекающими с верхней и нижней поверхностей крыла. Вследствие особой формы крыла эти потоки имеют разные скорости, поэтому поверхность раздела превращается в вихрь (циркуляцию), который отрывается и уносится вместе с потоком. Однако у крыла остаётся циркуляция противоположного направления, т. к. согласно теореме Томсона (Кельвина) общая сумма циркуляций скорости вдоль замкнутой жидкой линии должна оставаться постоянной.

Формула Жуковского получена для плоскопараллельного движения крыла бесконечного размаха. Для отрезка крыла длиной $L$ подъёмная сила $Y=ρv_∞ΓL$. Так как величина $Γ$ имеет размерность $[v_∞l]$, где $l$ – длина хорды крыла, то подъёмную силу можно записать в виде $Y=(1/2)C_yS\rho v^2_{\infty}$, где $S$ – характерная величина площади тела (например, площадь крыла в плане), $C_y$ – безразмерный коэффициент подъёмной силы. Эта формула применима при обтекании произвольных тел как вязкой, так и невязкой жидкостью, а также газом. Коэффициент $C_y$ в общем случае зависит от числа Рейнольдса, числа Маха $M_∞$, угла атаки $α$, угла стреловидности, формы крыла. Коэффициент $C_y$ определяется экспериментально или численным решением задач обтекания. Согласно теории Жуковского, для крыла в плоскопараллельном потоке $C_y=2m(α-α_0)$, где $α_0$ – угол атаки, при котором подъёмная сила равна нулю, $m$ – коэффициент, зависящий только от формы профиля крыла (например, для тонкой изогнутой пластины $m=π$). Учёт вязкости жидкости уменьшает множитель $m$ и, соответственно, подъёмную силу. Это связано с появлением в вязкой жидкости пограничного слоя, вследствие чего происходит отрыв потока, на профиле образуется область возвратного течения с почти постоянным давлением, что приводит к уменьшению подъёмной силы. При увеличении угла атаки зависимость $C_y(α)$ перестаёт быть линейной. При угле атаки, называемом критическим, значение $C_y$ достигает максимума (и уменьшается при дальнейшем росте $α$). Величина максимального значения $C_y$ играет важную роль в аэродинамике: чем она больше, тем меньше скорость взлёта и посадки самолёта. При больших скоростях становится существенной сжимаемость газа.

При сверхзвуковых скоростях характер обтекания тел существенно меняется. Так, при обтекании плоской пластины идеальным газом у передней кромки сверху образуется т. н. веер разрежения с уменьшением давления за ним, а снизу – ударная волна с повышением давления за ней. В результате давление на нижней поверхности пластины $p_н$ становится больше, чем на верхней $p_в$, т. е. возникает подъёмная сила. Для чисел Маха, незначительно превышающих 1, и малых $α$ коэффициент подъёмной силы пластины может быть вычислен по формуле Аккерета: $C_y=4/\alpha\sqrt{M^2_{\infty}-1}$. Эта формула справедлива для тонких профилей произвольной формы с острой передней кромкой. Разработаны численные методы решения задач сверхзвукового обтекания тел произвольной формы как в рамках решения уравнений Эйлера (идеальный газ), так и в рамках решения уравнений Навье – Стокса и Рейнольдса с учётом физико-химических свойств газа.

Важной характеристикой крыла, применяемой для расчёта подъёмной силы, является т. н. поляра крыла – график зависимости полной аэродинамической силы от угла атаки. Точки на поляре дают значения коэффициента $C_y$ и коэффициента сопротивления $C_x$, отвечающих одному и тому же углу атаки. Отношение $K=C_y/C_x$ называется аэродинамическим качеством крыла. Эта величина является одной из основных характеристик, определяющих совершенство самолёта. Так, крылья альбатроса (размах которых достигает 4 м, а развиваемая птицей скорость – 110 км/ч) имеют коэффициент качества 20. Эту величину авиаконструкторам удалось превзойти лишь при создании планёров и высотных (военных, спортивных) самолётов.

Подъёмная сила крыла конечного размаха имеет свои качественные особенности: течение около такого крыла интерпретируется как присоединённая вихревая нить, которая на концах крыла сходит и образует в следе за крылом два конечных (пограничных) вихря, которые соединяются с начальным вихрем, уходящим в бесконечность, образуя подковообразный вихрь. Эти вихри вызывают появление индуцированной компоненты скорости за крылом, направленной вниз по потоку. Л. Прандтль использовал схему подковообразного крыла для расчёта индуцированной подъёмной силы с учётом распределения циркуляций $Γ(y)$ по крылу конечного размаха (т. н. переменная циркуляция). Величина $Γ(y)$ находится из решения основного интегро-дифференциального уравнения теории крыла Прандтля, и затем подъёмная сила рассчитывается по формуле $Y=pv_{\infty}\int_{-L/2}^{L/2}Γ(y)dy$, где $L$ – размах крыла.