Механи́зм Хи́ггса (механизм Браута – Энглера – Хиггса) в теории калибровочных полей, состоит в поглощении безмассовых скалярных частиц, возникающих при спонтанном нарушении глобальной симметрии (т. н. голдстоуновских бозонов), безмассовыми векторными частицами, которые являются квантами калибровочных полей группы локальной симметрии. При этом голдстоуновские бозоны становятся дополнительно продольными компонентами векторных частиц, в результате чего последние приобретают массу. Таким образом, из спектра частиц исчезают безмассовые состояния и появляются массивные векторные бозоны, которые в случае ненарушенной симметрии были бы безмассовыми. Механизм Хиггса используется в Стандартной модели фундаментальных взаимодействий для объяснения появления массы у промежуточных векторных W- и Z- бозонов – переносчиков слабых взаимодействий. Помимо этого, в результате спонтанного нарушения симметрии появляются массы у кварков и лептонов, которые тоже являются безмассовыми, если симметрия не нарушена.

Стандартная модель

Современная теория элементарных частиц – Стандартная модель фундаментальных взаимодействий – строится на основе понятия симметрии. Это не только хорошо знакомая пространственная симметрия, а симметрия относительно преобразований в т. н. внутреннем пространстве, как, например, симметрия относительно фазовых преобразований или относительно вращений в пространстве изотопического спина, или в пространстве «цвета». Согласно Стандартной модели, весь материальный мир построен из частиц двух сортов: кварков и лептонов. Из кварков построены протоны и нейтроны, из которых состоят ядра атомов, а легчайший лептон – электрон, образует атомную оболочку. Всего известно шесть сортов кварков и столько же сортов лептонов. Их обычно подразделяют на три поколения, которые полностью идентичны, за исключением значений их масс. Каждое последующее поколение тяжелее, чем предыдущее. Все эти частицы открыты экспериментально на ускорителях в 20 в.

Кварки и лептоны участвуют в трёх фундаментальных взаимодействиях: сильном, слабом и электромагнитном. Существует ещё гравитация, но она очень слаба, и ею обычно пренебрегают в физике микромира. Все эти взаимодействия осуществляются путём обмена квантами соответствующего поля: глюонами, промежуточными векторными бозонами и фотонами соответственно. Симметрии, связанные с этими тремя взаимодействиями, формулируются на языке теории групп и отвечают преобразованиям в соответствующем пространстве параметров. Уравнения, которыми описываются кварки и лептоны, а также частицы – переносчики взаимодействий, должны быть инвариантны относительно преобразований симметрии. Это требование есть следствие тех законов сохранения, которые были проверены экспериментально. Конкретный вид групп симметрии – это также вопрос соответствия теории с экспериментом. В результате многолетних усилий были установлены группы симметрии трёх фундаментальных взаимодействий. Этими группами являются, соответственно, специальные унитарные группы SU(3), SU(2) и унитарная группа U(1).

Парадокс массы

Наличие симметрий уравнений движения для частиц не только приводит к законам сохранения, например, электрического заряда или «цветного» кваркового заряда, но и определяет свойства их взаимодействий, разрешённые моды (каналы) распада, времена жизни, и т. д. Таким образом, вид симметрии является определяющим при формулировке модели фундаментальных взаимодействий. Однако перечисленные группы симметрии Стандартной модели запрещают существование масс у кварков, лептонов и частиц – переносчиков взаимодействий. В то же время известно, что безмассовыми являются лишь фотон и глюон – переносчики электромагнитных и сильных взаимодействий соответственно, а все другие частицы обладают массой.

Для разрешения указанного парадокса требуется наличие механизма нарушения симметрии, однако такого, чтобы он не разрушил те свойства частиц, которые твёрдо установлены экспериментально. Следует ещё отметить, что теория, которая описывает элементарные частицы, является квантовой теорией поля – обобщением квантовой механики на системы с бесконечным числом степеней свободы. Для своей математической согласованности квантово-полевая Стандартная модель фундаментальных взаимодействий с необходимостью должна обладать симметрией.

Спонтанное нарушение симметрии

Для обоснования наличия масс у кварков, лептонов и частиц – переносчиков взаимодействий был предложен т. н. механизм спонтанного нарушения симметрии, известный в статистической физике, но приобретший новые черты в релятивистской физике элементарных частиц. Дело в том, что спонтанное нарушение симметрии обычно сопровождается появлением безмассовых состояний, которые не наблюдаются в физике частиц. Однако оказалось, что в данном случае эти безмассовые состояния являются фикцией и на самом деле являются продольными модами векторных бозонов – переносчиков слабого взаимодействия. Механизм спонтанного нарушения симметрии с поглощением безмассовых мод в продольные состояния векторных бозонов иногда называют механизмом Хиггса в честь П. Хиггса, одного из авторов данной идеи (Нобелевская премия 2013 г.). Стоит отметить, что первые опубликованные работы, где был предложен этот механизм, принадлежат американо-бельгийскому физику Роберту Брауту, бельгийцу Франсуа Энглеру и шотландцу Питеру Хиггсу. К этому же выводу независимо пришли американцы Джералд Гуральник, Карл Хаген и британец Томас Киббл.

Идея спонтанного нарушения симметрии состоит в том, что дифференциальные уравнения движения остаются неизменными и определяются ненарушенной симметрией теории, а нарушение касается только начальных условий.

Пример: рассадка гостей за круглым столом, когда перед каждым гостем стоит прибор, между каждыми двумя приборами лежит салфетка. Ситуация полностью симметрична относительно вращений стола. При большом количестве гостей группа симметрии вращений круглого стола есть группа U(1), которая является группой электромагнитных взаимодействий. Если один гость выбирает салфетку либо справа, либо слева от себя, то симметрия нарушается. Таким образом, при сохранении симметрии круглого стола и всей рассадки гостей начальные условия  нарушили симметрию относительно группы вращений.

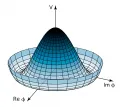Потенциал поля Хиггса.Потенциал поля Хиггса.Как использовать данный механизм в Стандартной модели фундаментальных взаимодействий и почему он позволяет придать массу всем частицам? Прежде всего в модель вводится дополнительное поле спина 0. Таких полей в Стандартной модели не было: все кварки и лептоны имеют спин 1/2, все переносчики взаимодействий – спин 1. Затем предполагается, что потенциал имеет такой вид, что низшее энергетическое состояние соответствует ненулевому среднему значению поля. В Стандартной модели потенциал выбирается в форме, напоминающей донышко бутылки из-под шампанского, или в форме мексиканской шляпы (рис.). В этом случае положение в центре является неустойчивым, а устойчивым низшим состоянием является положение вдоль жёлоба, окружающего центр. Потенциал при этом симметричен относительно вращений вокруг оси, проходящей через центр (в Стандартной модели это соответствует группе симметрии слабых взаимодействий), но, если выбрать какое-либо положение на жёлобе, то это нарушит вращательную симметрию. Другими словами, осуществляется спонтанное нарушение симметрии: уравнения движения симметричны, а начальное значение – среднее значение поля – нарушает симметрию. Это среднее значение – конденсат – является величиной постоянной, не зависящей от точки пространства и времени. Это как бы некая среда, в которую погружены все частицы Стандартной модели.

Механизм генерации масс

Распространяясь в пространстве, частицы взаимодействуют с постоянным полем как с некоторой вязкой средой, что приводит к замедлению их движения, тем больше, чем сильнее взаимодействие. Тем самым они приобретают массу, пропорциональную силе взаимодействия с этой средой. Отношения масс различных частиц должно быть пропорционально отношению соответствующих констант, характеризующих силу взаимодействия. В случае частиц – переносчиков слабого взаимодействия, т. н. W- и Z-бозонов, а также тяжёлых кварков и лептонов это предсказание блестяще выполняется.

Тем самым все частицы, взаимодействующие с этим новым полем, приобретают массу. Это относится к кваркам, лептонам и W- и Z-бозонам. Фотон и глюон с этим полем не взаимодействуют и остаются безмассовыми. Соответственно группа симметрии Стандартной модели SU(2) становится нарушенной, а ненарушенными остаются группы SU(3) и U(1).

Хиггсовский бозон

Однако проявлением существования нового поля является не только конденсат. В квантовой теории каждому полю соответствуют квантовые флуктуации, проявляющиеся как частицы. Частицей, соответствующей данному новому полю, и является бозон Хиггса – частица спина 0. Хиггсовский бозон тоже приобретает массу в результате взаимодействия с той же самой средой, так что она тоже пропорциональна силе этого взаимодействия. Но, так как теория не предсказывает значение константы самодействия бозона Хиггса, не предсказывается и его масса.

Хиггсовский бозон был экспериментально обнаружен на Большом адронном коллайдере в Европейском центре ядерных исследований (ЦЕРН) в Женеве (4 июля 2012). Его масса оказалась равной 125,5 ГэВ. Масса бозона Хиггса не предсказывается теорией, но определяется из эксперимента. Было подтверждено, что константы взаимодействия хиггсовского бозона с кварками и лептонами пропорциональны их массам. Тем самым экспериментально подтверждён механизм спонтанного нарушения симметрии.