Экстрема́льный граф, граф, на котором та или иная числовая характеристика принимает своё минимальное или максимальное значение. Обычно отыскиваются экстремальные значения некоторой одной числовой характеристики при ограничениях на другие числовые характеристики и свойства. Часто задача состоит в описании множества соответствующих экстремальных графов. Пусть, например, зафиксированы целые положительные числа $n$ и $k$ и отыскивается наибольшее число рёбер $n$-вершинного графа, не имеющего полных подграфов с $k+1$ вершинами. Установлено, что это число равно $$\frac{k-1}{2k}\left(n^2-r^2\right)+\frac{r(r-1)}2,$$где $n=k\left[\dfrac nk\right]+r$. При этом единственным с точностью до изоморфизма экстремальным графом является полный $k$-дольный граф, мощности долей которого отличаются не более чем на единицу (P. Turán, 1954).

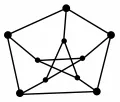Рис. 1. Граф Петерсена.Рис. 1. Граф Петерсена.На экстремальных графах изучаемые числовые характеристики достигают своего глобального экстремума. Так называемые критические графы могут рассматриваться как локально оптимальные. Пусть заданы некоторое свойство $A$ и набор одноместных операций $O_1,\ldots, O_s$ над графами. Граф $G$, обладающий свойством $A$, называется критическим по свойству $A$ относительно операций $O_1,\ldots, O_s$, если после применения любой из этих операций получается граф, не обладающий свойством $A$. При этом предполагается, что множество графов, не обладающих свойством $A$, замкнуто относительно рассматриваемых операций. В качестве свойства $A$ рассматриваются такие свойства графа, как быть связным, плоским, $k$-хроматическим и т. п., а в качестве операций – операции удаления и добавления вершины или ребра, стягивания ребра и др. Например, граф Петерсена (см. рис. 1) является критическим по свойству иметь рёберное хроматическое число, равное $4$, относительно операции удаления ребра.

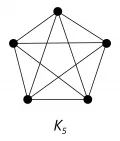Рис. 2. Полный граф с пятью вершинами.Рис. 2. Полный граф с пятью вершинами.Полный пятивершинный граф $K_5$ (рис. 2) и полный двудольный граф $K_{3,3}$ (рис. 3), каждая доля которого имеет три вершины, являются критическими по свойству не быть плоским относительно операций удаления ребра, стягивания ребра, удаления вершины.

При изучении свойств и характеристик графов оказывается полезным изучение их критических подграфов, т. е. подграфов, обладающих теми или иными свойствами и являющихся минимальными (максимальными) по включению. Примеры таких подграфов – компоненты связности ($k$-связности), остовные деревья.

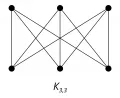Рис. 3. Полный двудольный граф с тремя вершинами в каждой доле.Рис. 3. Полный двудольный граф с тремя вершинами в каждой доле.Экстремальные и критические графы служат: для описания классов графов, обладающих заданными свойствами и числовыми характеристиками; для установления взаимосвязи между различными свойствами и числовыми характеристиками; для проверки наличия того или иного свойства графа.