Двудо́льный граф (бихроматический граф), граф, множество вершин которого $V$ можно разбить на два непересекающихся подмножества $V'$ и $V''$ (т. е. $V=V'\cup V''$, $V'\cap V''=\varnothing$) так, что каждое ребро соединяет некоторую вершину из $V$ с некоторой вершиной из 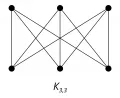$V''$. Полный двудольный граф с тремя вершинами в каждой доле.Полный двудольный граф с тремя вершинами в каждой доле.Граф является двудольным тогда и только тогда, когда все его простые циклы имеют чётную длину. Под двудольным графом часто понимают также граф, в котором заранее заданы подмножества вершин $V'$ и $V''$ (доли). Двудольные графы удобны для представления бинарных отношений между элементами двух разных типов, например: взяв элементы данного множества и его подмножества, имеем отношение «вхождение элемента в подмножество»; для исполнителей и видов работ имеем отношение «данный исполнитель может выполнять данную работу» и т. д.

Среди задач о двудольных графах важное место занимает изучение паросочетаний, т. е. семейств попарно несмежных рёбер. Такие задачи возникают, например, в теории расписаний (разбиение рёбер двудольного графа на минимальное число непересекающихся паросочетаний), в задаче о назначениях (нахождение максимального паросочетания) и т. д. Мощность максимального паросочетания в двудольном графе равна

$$|V'|-\max_{A'\subseteq V'}\bigl(|A'|-|V''(A')|\bigr),$$где $V''(A')$ – число вершин из $V''$, смежных хотя бы с одной вершиной из $A'$. Полный двудольный граф – это двудольный граф, в котором любые две вершины из различных подмножеств соединены ребром (например, граф $K_{3,3}$, см. рис.). Обобщением понятия «двудольный граф» является понятие «$k$-дольного графа», т. е. графа, в котором вершины разбиты на $k$ подмножеств так, что каждое ребро соединяет вершины из разных подмножеств.