Золото́е сече́ние (гармоническое деление, деление в крайнем и среднем отношении), деление отрезка $a$, при котором бо́льшая часть $x$ является средней пропорциональной между всем отрезком $a$ и меньшей его частью $a-x$, т. е.

$$\tag{*} a:x=x:(a-x).$$Для нахождения $x$ получается квадратное уравнение

$$x^2+ax-a^2=0,$$решение которого даёт

$$x =\frac a2\left(\sqrt{5}-1\right) \approx 0{,}62a.$$Условие (*) можно переписать и так:

$$\begin{gathered} \frac xa\left(1+\frac xa\right)=1\quad\text{или}\quad x=\cfrac{a}{1+\cfrac xa},\\ x=a\,\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\ldots,}}}} \end{gathered}$$т. е. $x$ получают в виде непрерывной дроби, подходящие дроби которой будут:

$$\frac 11,\ \frac 12,\ \frac 23,\ \frac 35,\ \frac 58,\ \frac8{13},\ \frac{13}{21}\ \text{ и т. д.,}$$где $1, 1, 2, 3, 5, 8, 13, 21$ и т. д. – т. н. числа Фибоначчи.

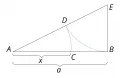Деление отрезка в крайнем и среднем отношении (золотое сечение).Деление отрезка в крайнем и среднем отношении (золотое сечение).Геометрически золотое сечение отрезка $AB$ (см. рисунок) строится так: в точке $B$ восстанавливают перпендикуляр к $AB$, откладывают на нём отрезок $BE=\frac 12AB$, соединяют $A$ и $E$, откладывают $ED=EB$ и, наконец, $AC=AD$, тогда

$$AB : AC=AC : CB.$$Золотое сечение было известно ещё в древности. В дошедшей до нас античной литературе оно впервые встречается в «Началах» Евклида.

Термин «золотое сечение» ввёл Леонардо да Винчи. Принципы золотого сечения или близкие ему пропорциональные отношения легли в основу композиционного построения многих произведений мирового искусства (главным образом произведений архитектуры Античности и Возрождения).