Солнечное динамо
Со́лнечное дина́мо, физический процесс, обусловливающий формирование и изменения во времени солнечных магнитных полей (солнечный магнетизм), включая 11-летний цикл солнечной активности (цикл Швабе). Солнечные магнитные поля генерируются благодаря взаимодействию течений солнечной плазмы, имеющей высокую электрическую проводимость, с магнитными полями, существующими в области течения. Физической сутью солнечного динамо является переход кинетической энергии движения плазмы в магнитную энергию благодаря комплексу электромагнитных и механических процессов, среди которых важнейшую роль играет электромагнитная индукция. При движении солнечной плазмы в магнитном поле благодаря электромагнитной индукции возникает электрический ток, который в свою очередь создаёт новое магнитное поле.
Солнечное динамо является частным случаем гидромагнитного динамо, которое действует не только на Солнце, но и в дисках спиральных галактик, звёздах, Земле (геодинамо), планетах и т. д. Различные виды динамо имеют свою специфику, поскольку очень разнообразны физические условия в этих небесных телах. Начиная с рубежа 20–21 вв. динамо воспроизводят в лабораторных условиях (см., например: Соколов. 2014).
Термин «динамо» отражает глубокую аналогию между процессами, протекающими в небесных телах при формировании их магнитных полей и в динамо-машине, которая присутствует в самых разнообразных технических устройствах (именно динамо-машины на электростанциях вырабатывают электрический ток). По сложившейся традиции, этот термин часто употребляют в расширенном значении – по отношению не только к процессу, но и к самому движению проводящей среды.
Модель солнечного динамо требуется не столько для объяснения самого факта существования магнитного поля Солнца, сколько для объяснения характера его изменений во времени. Из современных теоретических представлений и наблюдательных данных гелиосейсмологии следует, что внутри Солнца существует область, состоящая из хорошо проводящей плазмы и вращающаяся как твёрдое тело. Согласно законам электродинамики, магнитное поле в такой области может существовать без значительного затухания на протяжении времени, сопоставимого с возрастом Солнца. Возможно, такая компонента солнечного магнитного поля действительно присутствует (т. н. реликтовое магнитное поле), однако она не может обеспечивать поверхностную магнитную активность Солнца, в том числе солнечный цикл, поскольку в ходе этого цикла магнитное поле Солнца меняет знак каждые 11 лет (правило полярности Хейла).
Идея о том, что формирование магнитного поля Солнца может быть обусловлено только электромагнитной индукцией, была высказана Дж. Лармором в 1919 г. (Larmor. 1920), т. е. практически сразу же после обнаружения магнитного поля солнечных пятен в первом десятилетии 20 в. Основной трудностью в физической реализации идеи Лармора является то, что по правилу Ленца, магнитное поле, порождаемое электромагнитной индукцией в движущемся контуре, направлено противоположно исходному магнитному полю. Поэтому для реализации динамо необходимо использовать как минимум два электрических контура, так, чтобы индукция первого контура усиливала магнитное поле во втором контуре, а индукция второго контура – в первом. Очевидно, что движение проводящей среды, которое может обеспечить подобный процесс, должно быть достаточно сложным.
Первая реалистичная схема движения плазмы в условиях Солнца была предложена в 1955 г. Ю. Паркером (Parker. 1955). Он заметил, что во вращающемся теле со стратификацией плотности (т. е. плотность которого меняется с расстоянием от центра) из-за действия силы Кориолиса конвекция и турбулентность становятся зеркально-асимметричными, т. е. среднее число лево- и правовращающихся конвективных или турбулентных вихрей становится различным. Это означает, что при описании солнечной конвекции и турбулентности приходится использовать псевдоскалярные величины, знак которых зависит от того, какая система координат используется – правая или левая. При отражении в зеркале правая система координат переходит в левую, левовращающиеся вихри – в правовращающиеся, а псевдоскалярные величины меняют знак.
Предложенное Паркером объяснение зеркальной асимметрии движений солнечной среды как результата действия силы Кориолиса не является единственным. Зеркальная асимметрия может возникать и в результате воздействия на среду магнитной силы (которая является следствием действия силы Лоренца). В этом случае зеркальная асимметрия возникает у крупномасштабных движений среды (т. н. динамо Бэбкока – Лейтона). В настоящее время считается, что этот механизм играет более важную роль на Солнце, чем действие силы Кориолиса.
Наличие псевдоскалярных величин приводит к возникновению в уравнении электромагнитной индукции членов, описывающих рост и последующие осцилляции магнитного поля во времени. Как правило, различие в среднем числе лево- и правовращающихся вихрей невелико (порядка 10%), однако оно позволяет получить компоненту электрического тока, которая параллельна (а не перпендикулярна, как обычно) магнитному полю. Это, в свою очередь, позволяет вопреки правилу Ленца получить растущее магнитное поле.
Паркер пользовался интуитивными, но, как показало дальнейшее развитие науки, качественно правильными аргументами. Теоретическая база для описания динамо в астрофизических объектах была разработана в 1965 г. М. Штеенбеком, Ф. Краузе и К.-Х. Редлером (ГДР). В их работах вводятся понятия среднего магнитного поля, среднего тока и других средних величин, под которыми подразумеваются величины, усреднённые по флуктуациям движения среды. Для этих средних величин выводятся уравнения электродинамики средних полей, из которых следует, что у среднего электрического тока возникает компонента, параллельная среднему магнитному полю. Это явление получило название альфа-эффекта.
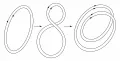Рис. 1. «Восьмёрка Зельдовича». Замкнутая петля магнитного поля растягивается вдвое, далее складывается в «восьмёрку», и обе половины «восьмёрки» накладываются друг на друга с переворотом. Диссипация превращает эти два витка в один, несущий увеличенный магнитный поток.Двумя другими идеями, на которых основана теория солнечного динамо, являются: 1) восходящее к работам Х. Альвена представление о вмороженности полного (а не среднего) магнитного поля в движущуюся, хорошо проводящую среду; 2) объяснение роста магнитного потока несмотря на вмороженность магнитного поля. Последнее объяснение было предложено Я. Б. Зельдовичем и иллюстрируется «восьмёркой Зельдовича»: замкнутая петля магнитного поля растягивается вдвое, далее складывается в «восьмёрку» и две части «восьмёрки» накладываются друг на друга с переворотом так, чтобы магнитные потоки в этих частях складывались, а не вычитались (рис. 1). При этом диссипативные процессы сглаживают мелкие детали пространственного распределения магнитного поля.
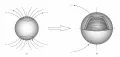Рис. 2. Формирование тороидального магнитного поля Солнца из полоидального вследствие дифференциального вращения Солнца: (а) наружные отрезки силовых линий исходного полоидального поля, проходящих сквозь конвективную зону Солнца и выходящих в атмосферу; (б) силовые линии формируемого тороидального поля в конвективной зоне.Основанное на этих идеях объяснение работы солнечного динамо выглядит следующим образом. Магнитное поле представляется в виде векторной суммы двух компонент – полоидальной, лежащей в плоскости солнечного меридиана (и подобной магнитному полю магнитного диполя), и тороидальной, направленной вдоль солнечной параллели. Неоднородное (дифференциальное) вращение Солнца формирует («вытягивает» в силу вмороженности) тороидальную компоненту магнитного поля из полоидальной (рис. 2). Далее, восходящие и нисходящие конвективные потоки солнечного вещества приводят к образованию изгибов или петель силовых линий магнитного поля (рис. 3, а, б) с последующим поворотом этих петель вследствие действия силы Кориолиса на поток (рис. 3, б в). В результате из тороидального магнитного поля снова образуется полоидальное (рис. 3, г).
Рис. 3. Восстановление полоидального магнитного поля из тороидального вследствие альфа-эффекта.
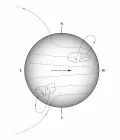Рис. 4. Выход магнитных петель на поверхность Солнца, приводящий к образованию групп солнечных пятен. Буквами «г» и «х» обозначены соответственно головное (ведущее) и хвостовое (ведомое) пятна группы. Горизонтальная стрелка показывает направление вращения Солнца.Образующиеся в ходе этого процесса петли магнитных силовых линий могут выходить на поверхность Солнца и приводить к образованию групп солнечных пятен (рис. 4). Рис. 3 иллюстрирует локальный процесс, приводящий к образованию полоидальной компоненты магнитного поля. В каждом из таких локальных процессов образующиеся компоненты поля могут иметь разные направления (другими словами, альфа-эффект может иметь разные знаки). Общее полоидальное поле создаётся ансамблем большого числа движущихся элементарных объёмов вещества, часть которых даёт альфа-эффект одного знака, часть – другого. Результирующее поле образуется как средний эффект этих процессов.
Тот же самый процесс можно описать, оперируя понятием электрического тока, а не силовых линий магнитного поля. Можно себе представить, что полоидальное и тороидальное магнитные поля созданы электрическими токами двух замкнутых проводящих контуров. При этом магнитное поле каждого из контуров вследствие электромагнитной индукции усиливает электрический ток во втором контуре и, следовательно, приводит к увеличению его магнитного поля. Подобное взаимное усиление магнитных полей двух контуров позволяет обойти запрет на рост магнитного поля в силу правила Ленца. Как видно из рис. 3, г, полоидальная компонента магнитного поля, полученная из тороидальной, порождается компонентой электрического тока, которая образовалась в результате этого процесса и направлена вдоль исходного тороидального магнитного поля (это и есть альфа-эффект).
В настоящее время альфа-эффект измерен в лабораторных условиях в Институте механики сплошных сред Уральского отделения РАН (Пермь) (см., например: Соколов. 2014).
Уравнения, описывающие солнечное динамо, при подходящем выборе параметров задачи имеют решения в виде волн квазистационарного магнитного поля, бегущих от средних широт к солнечному экватору (динамо-волны). Изображение этих волн на широтно-временной диаграмме похоже на баттерфляй-диаграмму солнечных пятен, описывающую структуру цикла Швабе солнечной активности и правило полярности Хейла. Если пренебречь влиянием магнитного поля на движение плазмы (кинематическое приближение), то амплитуда магнитного поля, осциллируя, экспоненциально растёт со временем. Учёт влияния магнитного поля на движение (прежде всего, альфа-эффекта) позволяет получить стационарные бегущие волны.
Для достижения количественного соответствия между моделями солнечного динамо и данными наблюдений необходимо учесть ряд других физических эффектов, дополняющих работу основного механизма динамо, – прежде всего, меридиональную циркуляцию солнечного вещества.
Описание работы солнечного динамо на языке электродинамики средних полей не является единственным возможным. Методы современной вычислительной физики позволяют избежать усреднения магнитного поля по ансамблю конвективных вихрей и работать непосредственно с полным магнитным полем, не вводя представление об альфа-эффекте и другие представления электродинамики средних полей. При этом модели солнечного динамо различных уровней детальности дополняют друг друга, раскрывая различные стороны этой сложной задачи.
Работа динамо происходит в глубине Солнца – области недоступной прямым наблюдениям. Поэтому сопоставление модельных параметров и параметров, доступных наблюдению, является сложной задачей. В частности, очень трудно непосредственное измерение различных коэффициентов переноса, входящих в уравнения динамо, хотя в этой области в настоящее время наблюдается существенный прогресс (Степанов. 2019).
Представления о природе магнитных полей других небесных тел во многом сформировались под влиянием теории солнечного динамо (Соколов. 2014; Степанов. 2019).