Политопные перегруппировки
Полито́пные перегруппиро́вки (от поли... и греч. τόπος – место; политопальные перегруппировки), взаимные превращения между различными пространственными изомерами молекул состава MLx (M – центральный атом или атомный кластер, L – лиганды, х ⩾ 3), имеющими строение координационных полиэдров, – т. н. политопных изомеров (политопов). Термин «политопные перегруппировки» ввёл американский химик Э. Мюттертиз в 1969 г. Понятие о политопах в общем случае не связано с их реальным временем жизни.
Политопные перегруппировки протекают без разрыва химических связей в результате изменения углов политопа (изгибание) или длин его рёбер (растяжение-сжатие). Грани политопа – равносторонние треугольники и/или квадраты. Как правило, политоп, содержащий только треугольные грани, является основным (энергетически предпочтительным), все другие – альтернативными.
Основной политоп для х = 4 – правильный тетраэдр, х = 5 – тригональная бипирамида, х = 6 – правильный октаэдр, альтернативные политопы для х = 4 – квадрат, х = 5 – квадратная пирамида (1 квадратная грань), х = 8 – квадратная антипризма (2 квадратные грани) и т. д. В стереохимически нежёстких молекулах основные и альтернативные политопы энергетически близки друг другу. На рисунке представлены некоторые случаи политопных перегруппировок соединений MLx (стрелками показаны направления движения лигандов; C2v, Td и т. д. – группы симметрии молекул).
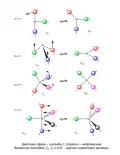 Политопные перегруппировки соединений MLₓ для x = 3–5.Экспериментально наиболее изучены политопные перегруппировки для систем с x = 3–5. При х = 3 путём политопных перегруппировок осуществляется пирамидальная инверсия (через промежуточную форму с плоской конфигурацией). В тетракоординационных системах, когда М – непереходный элемент, вероятность политопных перегруппировок крайне низка вследствие высокой устойчивости тетраэдрической формы (так, время жизни тетраэдрической молекулы метана оценивается в 1015 с).
Политопные перегруппировки соединений MLₓ для x = 3–5.Экспериментально наиболее изучены политопные перегруппировки для систем с x = 3–5. При х = 3 путём политопных перегруппировок осуществляется пирамидальная инверсия (через промежуточную форму с плоской конфигурацией). В тетракоординационных системах, когда М – непереходный элемент, вероятность политопных перегруппировок крайне низка вследствие высокой устойчивости тетраэдрической формы (так, время жизни тетраэдрической молекулы метана оценивается в 1015 с).
В то же время с высокой скоростью протекают политопные перегруппировки в системах, где М – переходный элемент, например в тетракоординационных комплексах Ni2+, Pt2+ (взаимные переходы квадратной и тетраэдрической структур). Широко представлены политопные перегруппировки в пентакоординационных системах, для которых разность энергий тригональной бипирамиды и квадратной пирамиды обычно весьма мала (например, в случае псевдовращения Берри в фосфоранах).
Для описания механизмов политопных перегруппировок используют теорию групп. Применяют 2 независимых способа: квантовохимические расчёты и метод Мюттертиза, основанный на анализе совокупности структурных данных о внутримолекулярных искажениях в однотипных системах (эти искажения отождествляют с механизмом политопных перегруппировок).
