Лист Мёбиуса, поверхность, получающаяся при склеивании двух противоположных сторон $AB$ и $A'B'$ прямоугольника $ABB'A'$ (рис. 1а) так, что точки $A$ и $B$ совмещаются

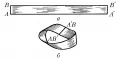Рис. 1. Построение листа Мёбиуса: а – исходный прямоугольник; б – лист Мёбиуса.Рис. 1. Построение листа Мёбиуса: а – исходный прямоугольник; б – лист Мёбиуса.соответственно с точками $B'$ и $A'$ (рис. 1б). Лист Мёбиуса был рассмотрен (1858–1865) независимо друг от друга немецкими математиками А. Мёбиусом и И. Листингом в качестве первого примера односторонней поверхности. Если двигаться вдоль по листу Мёбиуса, не пересекая его границы, то можно попасть в исходную точку, оказавшись в перевёрнутом положении по сравнению с первоначальным. Это связано с неориентируемостью листа Мёбиуса: если отметить на нём небольшую окружность, зафиксировать на ней направление обхода и двигать её вдоль листа Мёбиуса, не пересекая его границы, то можно прийти к начальному положению так, что направление обхода окружности изменится на противоположное. Этим же свойством обладает любая односторонняя поверхность.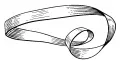Рис. 2. Поверхность, получаемая из листа Мёбиуса разрезанием его по средней линии.Рис. 2. Поверхность, получаемая из листа Мёбиуса разрезанием его по средней линии. Лист Мёбиуса ограничен одной замкнутой линией, поэтому если разрезать лист Мёбиуса по средней линии, то он не распадётся на две части, а превратится в поверхность гомеоморфную поверхности цилиндра, отличающуюся от неё лишь тем, что она дважды перекручена вокруг себя (рис. 2).

С топологической точки зрения лист Мёбиуса – неориентируемая поверхность с нулевой эйлеровой характеристикой, ограниченная одной замкнутой линией.