Лассо-регрессия
Лассо́-регре́ссия (англ. lasso или LASSO, least absolute shrinkage and selection operator), вариация линейной регрессии, которая используется в статистике и эконометрике для решения проблемы мультиколлинеарности (наличие линейной зависимости между объясняющими переменными) и отбора наиболее информативных (с точки зрения способности объяснять дисперсию зависимой переменной) признаков. В данном методе к задаче минимизации суммы квадратов остатков добавляется штраф на величину абсолютных значений параметров, который также называют -регуляризацией (regularization) или штрафом lasso. -регуляризация приводит к тому, что коэффициенты модели у наименее информативных признаков приравниваются к нулю. Это позволяет проводить отбор признаков в модели и сделать модель более интерпретируемой. Метод был предложен Р. Тибширани (род. 1956) в 1996 г.
Пусть есть выборка из наблюдений, которые состоят из зависимой (объясняемой) переменной и регрессоров (объясняющих переменных). Тогда оценка лассо-регрессии задаётся соотношением:
,
где – -ое наблюдение зависимой переменной, – -ое наблюдение -го регрессора, – свободный член, – коэффициенты модели, – параметр регуляризации.
Параметр накладывает штраф на сложность модели. При модель сводится к методу наименьших квадратов. Чем больше параметр , тем больше коэффициентов приравнивается к нулю.
Регрессоры должны быть стандартизованы, т. е. должны удовлетворять условиям:
.
Эквивалентный способ описать оценку регрессии lasso:
,
,
где – заранее заданный параметр, который определяет степень регуляризации.
Оценка лассо-регрессии, в отличие от другого способа решения проблемы мультиколлинеарности – гребневой регрессии, нелинейна по и не имеет аналитического решения. Задача поиска оптимальных коэффициентов для лассо-регрессии является задачей квадратичного программирования.
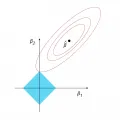 Оценка LASSO-регрессии с двумя регрессорами.На рисунке (Hastie. 2009. P. 71) изображён случай лассо-регрессии с двумя параметрами. Сумма квадратов остатков изображена в виде красных эллипсов с центром в точке, координаты которой соответствуют оценкам коэффициентов линейной регрессии без регуляризации. Голубая область – это штрафное ограничение . Решение для случая лассо-регрессии находится в точке касания контуров суммы квадратов остатков и границы голубой области. Как видно на графике, точка касания может находиться в углах ромба, т. е. некоторые коэффициенты будут приравниваться к нулю, а значение этой переменной не будет влиять на прогноз модели.
Оценка LASSO-регрессии с двумя регрессорами.На рисунке (Hastie. 2009. P. 71) изображён случай лассо-регрессии с двумя параметрами. Сумма квадратов остатков изображена в виде красных эллипсов с центром в точке, координаты которой соответствуют оценкам коэффициентов линейной регрессии без регуляризации. Голубая область – это штрафное ограничение . Решение для случая лассо-регрессии находится в точке касания контуров суммы квадратов остатков и границы голубой области. Как видно на графике, точка касания может находиться в углах ромба, т. е. некоторые коэффициенты будут приравниваться к нулю, а значение этой переменной не будет влиять на прогноз модели.
Для устранения недостатков лассо-регрессии на её основе были предложены модифицированные методы решения проблемы мультиколлинеарности, к примеру метод эластичной сети.
