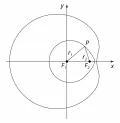
Дека́ртов ова́л, плоская кривая, расстояния $r_1$ и $r_2$ каждой точки $P$ которой до двух фиксированных точек $F_1$ и $F_2$ (фокусов) связаны неоднородным линейным уравнением$$r_{1}+m r_{2}=a.$$Декартов овал можно определить при помощи однородного линейного уравнения$$r_{1}+m r_{2}+n r_{3}=0,$$где $r_{3}$ – расстояние до третьего фокуса $F_{3}$, лежащего на прямой $F_1F_2$. Декартов овал в общем случае состоит из двух замкнутых линий, одна из которых объемлет другую (см. рис.). В прямоугольных декартовых координатах уравнение декартова овала имеет вид$$\sqrt{x^{2}+y^{2}}+m \sqrt{(x-d)^{2}+y^{2}}=a,$$где $d$ – длина отрезка $F_{1} F_{2}$. При $m=1$ и $a>d$ декартов овал представляет собой эллипс, при $m=-1$ и $a<d$ – гиперболу и, если $m=a/d$, – улитку Паскаля. Впервые декартов овал исследован Р. Декартом в связи с задачами оптики (см. Декарт. 1938).