Укла́дка гра́фа (вложение графа), отображение вершин и рёбер графа соответственно в точки и непрерывные кривые некоторого пространства такое, что вершины, инцидентные ребру, отображаются в концы кривой, соответствующей этому ребру. 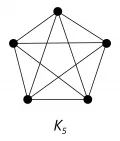Рис. 1. Полный граф с пятью вершинами.Рис. 1. Полный граф с пятью вершинами.Правильной укладкой называется укладка, при которой разным вершинам соответствуют различные точки, а кривые, соответствующие рёбрам (исключая их концевые точки), не проходят через точки, соответствующие вершинам, и не пересекаются. Любой граф допускает правильную укладку в трёхмерное пространство. Граф, допускающий правильную укладку на плоскости, называется плоским. Существуют неплоские графы, например графы $K_5$ (см. рис. 1) и $K_{3,3}$ (см. рис. 2). Наименьший род двумерной ориентируемой поверхности, на которой граф $G$ допускает правильную укладку, называется родом $\gamma(G)$ графа $G$. Установлено, в частности, что

$$\gamma(K_n)=\left]\frac{(n-3)(n-4)}{12}\right[,$$где $K_n$ – полный граф с $n$ вершинами, $\left]a\right[$ – наименьшее целое число, не меньшее $a$;

$$\gamma(K_{m,n})=\left]\frac{(m-2)(n-2)}{4}\right[,$$где $K_{m,n}$ – полный двудольный граф;

$$\gamma(Q_n)=1+(n-4)\cdot2^{n-3},$$где $Q_n$ есть $n$-мерный куб. Толщиной $\theta(G)$ графа $G$ называется наименьшее число его плоских подграфов, объединение которых даёт граф $G$. Установлено, в частности, что

$$\begin{gathered} \theta(K_p)=\left[\frac{p+7}6\right] \text{ при }p\neq9, 10;\quad \theta(K_9)=\theta(K_{10})=3,\\ \theta(Q_n)=\left]\frac{n+1}4\right[,\\ \theta(K_{m,n})=\left]\frac{mn}{2(m+n-2)}\right[ \end{gathered}$$(возможно с несколькими исключениями).

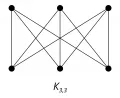Рис. 2. Полный двудольный граф с тремя вершинами в каждой доле.Рис. 2. Полный двудольный граф с тремя вершинами в каждой доле.Изучаются также другие числовые характеристики, связанные с укладкой графов, например число скрещиваний – наименьшее число пересечений рёбер, с которым можно уложить данный граф на данной поверхности; крупность – наибольшее число непересекающихся по рёбрам неплоских подграфов в данном графе и др. Рассматриваются также укладки на неориентируемых поверхностях. Вложение графа в $n$-мерную целочисленную решётку – это отображение в данную решётку, при котором вершины отображаются в различные узлы решётки, а рёбра идут по линиям решётки.

Задачи об укладках графов на поверхностях и вложениях их в решётки возникают при автоматизированном проектировании ЭВМ, при проектировании коммуникаций и т. д.