Предельный цикл системы дифференциальных уравнений
Преде́льный цикл систе́мы дифференциа́льных уравне́ний 2-го порядка
замкнутая траектория в фазовом пространстве , обладающая тем свойством, что все траектории, начинающиеся в достаточно узкой кольцеобразной её окрестности, неограниченно приближаются к этой траектории при (устойчивый предельный цикл) или при (неустойчивый предельный цикл) или часть из них при , а остальные – при (полуустойчивый предельный цикл). Например, система
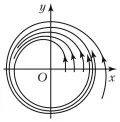
( и – полярные координаты), общее решение которой , , где , имеет устойчивый предельный цикл (рисунок). Понятие «предельный цикл» переносится и на системы -го порядка. С точки зрения механики устойчивый предельный цикл соответствует устойчивому периодическому движению системы. Поэтому поиск предельного цикла имеет важное значение в теории нелинейных колебаний.