Зо́нная тео́рия, квантовая теория, описывающая энергетический спектр электронов в периодическом потенциальном поле кристалла. Основы зонной теории были заложены Ф. Блохом (1928) и Л. Бриллюэном (1930). Согласно классической физике, при движении электрона (как и любой другой частицы) в периодическом потенциальном поле возможны две качественно различные ситуации. Если энергия электрона превышает максимальное значение потенциала поля, то электрон движется, периодически ускоряясь и замедляясь, с некоторой постоянной сравнительной скоростью. Если же энергия электрона достаточно мала, то он оказывается «запертым» в одном из минимумов потенциала и совершает в нём периодическое движение. При учёте квантовых эффектов электрон приобретает возможность туннелировать из одного минимума в другой и ситуация становится качественно одинаковой в обоих случаях: электрон может распространяться по всему кристаллу с постоянной в среднем скоростью, не испытывая никакого систематического ускорения или замедления. Поэтому периодический потенциал не является причиной конечного электрического сопротивления; последнее возникает лишь в результате отклонений от периодичности, связанных либо с тепловыми колебаниями атомов, либо с наличием примесей и дефектов. Однако распространение электрона по кристаллу оказывается возможным не при всех энергиях, а только в так называемых разрешённых зонах; последние отделены друг от друга так называемыми запрещёнными зонами, в которых движение электронов невозможно. Тем самым весь интервал энергий разбивается на совокупность чередующихся разрешённых и запрещённых зон. Характерная ширина энергетических зон составляет несколько электрон-вольт, что соответствует $10^4 К.$ Если объём кристалла конечен и содержит $N$ атомов, то в каждой разрешённой зоне имеется порядка $N$ квантовых состояний, которые можно понимать как густо расположенные энергетические уровни с примерно одинаковыми расстояниями между ними. Каждый уровень может быть занят лишь двумя электронами с противоположно направленными спинами (принцип Паули). При не слишком высоких температурах заполнение уровней происходит последовательно снизу вверх, начиная с самых нижних и до верхней границы заполнения – так называемого уровня Ферми $ℰ_F.$ При увеличении количества электронов уровень Ферми повышается. Уровень Ферми является резкой границей лишь при абсолютном нуле температуры, при конечной температуре он размыт на величину порядка $kT$ ($k$ – постоянная Больцмана, $T$ – абсолютная температура): верхние электроны могут приобретать дополнительную энергию теплового возбуждения и переходить на более высокие уровни. Распределение электронов по уровням может быть также изменено за счёт внешнего электрического поля, что приводит к направленному движению электронов и возникновению электрического тока. Наличие свободных состояний над уровнем Ферми – необходимое условие для протекания тока. Поэтому вещество является металлом и обладает хорошей проводимостью при любой (даже самой низкой) температуре, если уровень Ферми находится внутри разрешённой зоны (рис. 1, а). Если же количество электронов соответствует полному заполнению нескольких зон, то вещество является диэлектриком (рис. 1, б); верхняя из заполненных зон называется валентной зоной, а нижняя из незаполненных – зоной проводимости. В диэлектриках движение электронов возможно лишь в результате теплового возбуждения в более высокую разрешённую зону, что практически невозможно при обычных температурах.

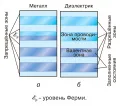Рис. 1. Схема заполнения зон.Рис. 1. Схема заполнения зон.Диэлектрики с узкой запрещённой зоной обычно называют полупроводниками – они обладают заметной проводимостью уже при комнатной температуре. Металлы, для которых уровень Ферми находится вблизи верхнего или нижнего края зоны, называют полуметаллами – их проводимость существенно ниже, чем у типичных металлов. К полуметаллам тесно примыкают так называемые легированные полупроводники, в которых уровень Ферми смещён в верхнюю или нижнюю разрешённую зону за счёт добавления примесей, поставляющих дополнительные электроны, – доноров, или примесей, локализующих на себе часть электронов проводимости, – акцепторов.

Полная энергия электрона в кристалле

$$E=p^2/2m+V(x)\tag1$$состоит из кинетической энергии (первое слагаемое) и потенциальной (второе); здесь $p=mv$ – импульс электрона, $m$ и $v$ – его масса и скорость, потенциал $V(x)$ является периодической функцией координаты $x$ [например, $V(x+a)=V(x)$ в одномерном случае]. Квантовая теория допускает другое описание, при котором потенциальная энергия явно не рассматривается, но учитывается за счёт модификации кинетической энергии, записываемой как $ε(p)$, при этом её зависимость от импульса – так называемый закон дисперсии (или спектр) – уже не имеет обычного квадратичного вида. Функция $ε(p)$ периодическая и в общем случае имеет несколько ветвей $ε_s(p),$ обозначаемых индексом $s.$ Например, в одномерном случае может оказаться, что

$$ε_1(p)=E_1+2J_1cos(pa/ℏ),\\ ε_2(p)=E_2+2J_2cos(pa/ℏ),\\ ............................\\ ε_s(p)=E_s+2J_scos(pa/ℏ),\tag 2$$где $ℏ$ – постоянная Планка, $a$ – параметр кристаллической решётки, $J_1,J_2,...,J_s$ – так называемые интегралы перекрытия. При изменении импульса кинетическая энергия электрона (совпадающая при этом описании с полной) пробегает интервалы $(E_1–2|J_1|,E_1+2|J_1|),(E_2–2|J_2|,E_2+2|J_2|),…,(E_s–2|J_s|,E_s+2|J_s|),$ которые и соответствуют разрешённым зонам. Уравнения движения электрона также существенно меняются. Вместо второго закона Ньютона $m \ddot{x} = F$ ($F$ – сила; штрихом обозначена производная по времени), который можно записать в виде $$\dot{p} = F, v = \dot{x} = p/m, \tag3$$справедливы уравнения $$\dot{p} = F, v = \dot{x} = dε(p)/dp, \tag4$$которые для квадратичного закона дисперсии $ε(p) = p^2 /2m$ совпадают с (3). Появление нетривиального закона дисперсии можно объяснить в двух предельных случаях, которые соответствуют приближениям сильной и слабой связи.

Рис. 2. Изолированная потенциальная яма и периодическое расположение ям.Рис. 2. Изолированная потенциальная яма и периодическое расположение ям.В методе сильной связи периодический потенциал представляют в виде совокупности слабо связанных потенциальных ям, периодически расположенных в пространстве. Согласно квантовой механике, изолированная потенциальная яма обычно имеет несколько дискретных уровней $E_1, E_2 ,$ … (рис. 2, а). При периодическом расположении таких ям (рис. 2, б) из-за туннелирования электрона между соседними ямами уровни расширяются в узкие зоны, в которых выполняются законы дисперсии (2). В этом предельном случае косинусоидальные зависимости строго обоснованы, а параметры $J_s$ пропорциональны вероятности туннелирования из ямы в яму для электрона в состоянии $s.$ В трёхмерном случае общий вид спектра сильной связи определяется выражением $$ε(p_x, p_y, p_z) = E_0 + 2J_xcos(p_xa/ℏ) + 2J_уcos(p_ya/ℏ) + 2J_zcos(p_za/ℏ).$$В приближении слабой связи за нулевое приближение принимается квадратичный спектр $p^2 /2m,$ а периодический потенциал $V(x)$ считается малым и рассматривается как возмущение. Под действием последнего спектр $p^2 /2m$ слегка искажается вблизи точек $pn = πℏn/a, n = ± 1, ± 2, …,$ для которых выполнено условие Брэгга – Вульфа (для простоты обсуждается одномерный случай); электроны испытывают брэгговские отражения, которые приводят к возникновению узких запрещённых зон (рис. 3, а). Парабола $p^2 /2m$ фактически «разрезается» на куски, концы которых слегка скругляются; куски затем периодически продолжаются на всю ось $p$ (рис. 3, б).

Рис. 3. Зонные схемы.Рис. 3. Зонные схемы.Для полного задания всех ветвей спектра их достаточно определить на интервале $−π/a < p/ℏ < π/a$ в так называемой первой зоне Бриллюэна. Уравнение $ε(p) = ℰ_F$ определяет в $p$-пространстве так называемую ферми-поверхность, которая для квадратичного спектра $p^2 /2m$ имеет сферическую форму. Для спектра (5) поверхность Ферми имеет вид эллипсоида при небольшом числе электронов в зоне. При увеличении числа электронов она начинает касаться границ первой зоны Бриллюэна, что с учётом периодического продолжения приводит к возникновению так называемой открытой поверхности Ферми. У щелочных металлов $(Li, K, Na, Rb, Cs)$ ферми-поверхности почти сферические, лишь слегка искажённые вблизи границ зоны Бриллюэна. У $Cu$ и благородных металлов $(Ag, Au)$ ферми-поверхности имеют вид сфер, соединённых узкими перемычками. Поверхности Ферми металлов $Al, Ga, Sn, Pb$ и других хорошо описываются приближением слабой связи; для их описания разработан так называемый метод псевдопотенциала. Поверхности Ферми и энергетические спектры переходных металлов очень сложны и не описываются простыми приближениями; они обычно вычисляются методом функционала плотности. Нетривиальный закон дисперсии и сложная форма поверхности Ферми проявляются во многих явлениях, которые одновременно являются способом их изучения: аномальном скин-эффекте, осцилляциях магнитной восприимчивости (эффект де Хааза – ван Альвена) и проводимости (эффект Шубникова – де Хааза), циклотронном резонансе, гальваномагнитных явлениях, магнитоакустических осцилляциях, размерных эффектах, радиочастотном эффекте Гантмахера, аннигиляции позитронов, форме линий комптоновского рассеяния, аномалиях Кона на кривых дисперсии фононов, определяемых с помощью неупругого рассеяния нейтронов. Основной метод изучения электронного спектра вдали от поверхности Ферми – метод рентгеновской фотоэмиссии. Аналогичным образом периодичность кристалла приводит к зонной структуре энергетического спектра всех квазичастиц (фононов, магнонов, экситонов и др.).