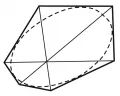
Теоре́ма Брианшо́на, теорема проективной геометрии, утверждающая, что во всяком шестиугольнике, описанном около конического сечения – эллипса (в частности, окружности), гиперболы, параболы, – прямые, соединяющие три пары противоположных вершин, проходят через одну точку (рис.). Теорема доказана французским математиком Ш.-Ж. Брианшоном (1806). Теорема Брианшона находится в тесной связи с теоремой Паскаля. Эти две теоремы устанавливают основные проективные свойства линий второго порядка.