Паралла́кс (от греч. παράλλαξις – отклонение), величина, равная видимому смещению светил на небесной сфере, обусловленному перемещением наблюдателя в пространстве. Чем ближе к наблюдателю располагается небесное тело, тем сильнее меняется направление на него при перемещении наблюдателя. Параллаксом также называют угол, под которым с небесного тела видно расстояние, на которое смещается наблюдатель. Точно измеренные параллаксы небесных светил и групп светил позволяют определять расстояния до них.

Суточный параллакс $p_с$ выражает изменение направления на небесное тело при воображаемом перемещении наблюдателя с поверхности в центр Земли или обратно:

$\sin{p_с}=(R/r)\sin{z},$

где $R\ -$ расстояние от наблюдателя до центра Земли, $r\ -$ расстояние от небесного тела до центра Земли, $z\ -$ зенитное расстояние небесного тела. 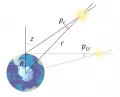Суточный параллакс.Суточный параллакс.Параллакс, определённый для наблюдателя, расположенного на экваторе, и небесного тела, находящегося на математическом горизонте $(z\!=\!90^\circ\!),$ называется суточным горизонтальным параллаксом $p_{сг}$ (в этом случае $R\ -$ экваториальный радиус Земли). Наибольший суточный горизонтальный параллакс имеет Луна – от 54′ до 61′. Важным параметром является суточный горизонтальный параллакс Солнца $\pi_\odot\!=\!8,\!80^{\prime\prime},$ поскольку его величина позволяет определить расстояние до Солнца через экваториальный радиус Земли. Величина $\pi_\odot,$ однозначно связанная с астрономической единицей, раньше рассматривалась в качестве одной из фундаментальных астрономических констант.

Для измерения расстояний до тел, находящихся вне Солнечной системы, используется годичный параллакс. Это угол $p_г,$ под которым с небесного тела виден барицентрический (с началом в барицентре $O_б$ Солнечной системы) радиус-вектор $\textbf{\textit{R}}_б$ центра масс системы «Земля – Луна»:

$\sin{p_г}=(R_б/r_б)\sin{E},$

где $r_б\ -$ расстояние от небесного тела до $O_б,$ $E\ -$ угол между вектором $\textbf{\textit{R}}_б$ и направлением на небесное тело из центра масс системы «Земля – Луна».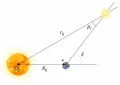Годичный параллакс.Годичный параллакс. Если угол $E$ прямой, то такой параллакс называется тригонометрическим параллаксом $p_т.$ Поскольку параллакс ближайших звёзд не превышает 1″, то $\sin{p_т}\approx p_т$ и $p_т\approx R_б/r_б.$ Таким образом, определение тригонометрического параллакса эквивалентно определению расстояния до небесного тела, которое может быть выражено через $R_б,$ равное 1 а. е.

Все звёзды в окрестностях Солнца обладают параллактическим движением, отражающим факт движения Солнца относительно центра Галактики. Величина $p_s\approx R_s/r_s$ называется вековым параллаксом, где $R_s\ -$ путь, пройденный Солнцем за год, $r_s\ -$ расстояние до звезды.

Измерение параллакса небесных тел, совместно с измерениями их небесных координат, даёт трёхмерную картину распределения этих тел в пространстве. Поэтому тригонометрический параллакс – один из важнейших астрометрических параметров, основа для всех других способов определения расстояний во Вселенной. В частности, через тригонометрический параллакс определяется внесистемная единица длины – парсек.

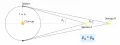Связь параллакса звезды с расстоянием до неё. Звезда А ближе к Солнцу, поэтому её параллакс больше.Связь параллакса звезды с расстоянием до неё. Звезда А ближе к Солнцу, поэтому её параллакс больше.Успешное выполнение космического проекта HIPPARCOS (1989–1993) позволило создать высокоточный каталог параллаксов около 120 тыс. звёзд и получить ценнейшую информацию о пространственном распределении этих звёзд в ближайшей окрестности Солнца (до 1 кпк). В 2013 г. запущен космический телескоп GAIA, цель которого – измерение координат и параллаксов около 1 млрд звёзд, что позволит построить трёхмерную карту почти всей Галактики. В середине 2022 г. был получен 3-й каталог (Gaia Data Release 3 – Gaia DR3), содержащий информацию о более чем 1,8 млрд объектов. Для 1,46 млрд объектов в диапазоне звёздных величин от 3-й до 21-й приводится полное астрометрическое решение – экваториальные координаты (α, δ), тригонометрические параллаксы и собственные движения. Ошибка измерения параллаксов ярких звёзд (до 15-й звёздной величины) равна 20–30 мкс дуги, т. е. расстояния измерены до 30–50 кпк.

Для оценки расстояний до очень далёких объектов используются менее точные (по сравнению с геометрическими) методы – определение т. н. спектрального параллакса, группового параллакса и статистического параллакса. Первый метод основывается на законе, утверждающем, что поток света от излучающего источника убывает обратно пропорционально квадрату расстояния до него. Определив спектральный класс и класс светимости звезды, можно оценить её истинную светимость (абсолютную звёздную величину). Затем, сравнивая абсолютную звёздную величину с видимой и учитывая межзвёздное поглощение света, можно оценить расстояние до звезды.

В методе группового параллакса измеряются собственные движения звёзд, входящих в звёздное скопление, а по ним – положение радианта скопления (точки, в которой пересекаются направления собственных движений звёзд скопления при продолжении их на небесной сфере). Если известны лучевые скорости звёзд (измеренные на основании эффекта Доплера), то, зная собственные движения звёзд и их угловое расстояние до радианта, можно рассчитать расстояние до каждой звезды движущегося скопления и среднее расстояние до скопления.

Метод статистического параллакса аналогичен методу группового параллакса, но применим только по отношению к достаточно большой и однородной группе звёзд, расстояние до которой оценивается на основании измерения их собственных движений, которые тем меньше, чем дальше находится эта группа.