Номогра́фия (от греч. νόμος – закон и ...графия), раздел математики, в котором изучаются способы графического представления функциональных зависимостей. Получающиеся при этом чертежи называются номограммами. Каждая номограмма строится для определённой функциональной зависимости в заданных пределах изменения переменных. ПРис. 1. Номография.Рис. 1. Номография.ри помощи номограмм вычислительную работу можно заменить выполнением простейших геометрических операций и считыванием ответов. Точность получения ответов по номограмме зависит от вида зависимостей между переменными, пределов изменения переменных, размеров чертежа и в среднем составляет 2–3 верные значащие цифры. Когда точность номограмм недостаточна, их можно использовать для прикидочных расчётов, для нахождения нулевых приближений, для контроля вычислений с целью обнаружения грубых ошибок.

Примерами номограмм являются график функции и двойная шкала, которая для уравнения $F(u,v)=0$ состоит из совмещённых шкал переменных $u$ и $v$. На рис. 1 изображена двойная шкала для вычисления десятичных логарифмов. На рис. 2 приведён пример номограммы для вычисления $\alpha_y$ – одного из углов установки резца на заточном станке по заданным значениям углов установки резца $\alpha$ и $\varphi$. Зависимость между этими величинами определяется формулой

$$\tg \alpha_y=\dfrac{\tg\alpha}{\sin \varphi}. \tag{*}$$Номограмма состоит из трёх шкал: шкалы углов $\alpha_y$, шкалы углов $\alpha$ и шкалы углов $\varphi$; она построена так, что три точки, соответствующие значениям углов $\alpha_y, \alpha, \varphi$, удовлетворяющих уравнению $(*)$, всегда лежат на одной прямой. 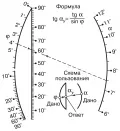Рис. 2. Номография. БРЭ. Т. 23.Рис. 2. Номография. БРЭ. Т. 23.Отсюда вытекает способ вычисления по номограмме: для вычисления $\alpha_y$ надо на шкалах $\alpha$ и $\varphi$ найти точки, соответствующие заданным значениям $\alpha$ и $\varphi$, и через эти точки провести прямую. Эта прямая пройдёт на шкале $\alpha_y$ через точку, соответствующую искомому значению $\alpha_y$. На рис. 2 пунктирная линия

соединяет точки шкал $\alpha$ и $\varphi$, со значениями $\alpha$=7,5° и $\varphi$=4°; номограмма для $\alpha_y$ даёт величину $\alpha_y$=62°.

С середины 1970-х гг. в связи с распространением электронной вычислительной техники номограммы стали выходить из употребления.