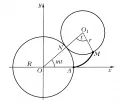
Эпицикло́ида, плоская кривая, траектория точки, производящей окружности радиуса $r$, катящейся без скольжения по другой неподвижной окружности радиуса $R$ вне её. На рис. 1 $O$ и $O_1$ – центры неподвижной и производящей окружностей, $N$ – точка их касания, $M$ –

вычерчивающая точка ($A$ – её исходное положение), $t$ – угол поворота производящей окружности, $AM$ – участок эпициклоиды.

Параметрические уравнения

$$x=(R+mR)\cos mt-mR\cos(t+mt),\\ y=(R+mR)\sin mt-mR\sin(t+mt),$$где $m=r/R$, $t$ – параметр. Форма кривой зависит от значения $m$ (на рис. 2а $m=1/3$, на рис. 

2б $m=2/3$). Если $m=p/q$, где $p$ и $q$ – взаимно простые числа, то точка $M$ после $q$ полных оборотов производящей окружности возвращается в исходное положение и эпициклоида – замкнутая кривая, состоящая из $q$ ветвей с $q$ точками возврата. При $m$ иррациональном множество ветвей бесконечно, точка $M$ в исходное положение не возвращается. См. также Эпитрохоида.

Рис. 1. Построение эпициклоиды.Рис. 1. Построение эпициклоиды.